Rechnen und rechnen lassen – Wie Simulationen die Lehre bereichern

Der Hypothesentest ist ein grundlegendes Mittel der Statistik, doch komplexe mathematische Formeln lassen viele Studierende scheitern. Dabei könnte die Vermittlung viel einfacher sein und dabei sogar genauere Ergebnisse liefern. Per Computer nämlich.

Mag sein, für faustische Charaktere, die wissen wollen, „was die Welt im Innersten zusammenhält“, mögen Hypothesentests weniger interessant sein. Aber alle, die sich dafür interessieren, wo auf dieser Welt blosser Zufall waltet und wo nicht, kommen um das Thema so wenig herum wie Studierende im Fach Statistik. Schliesslich lassen sich mit dem Hypothesentest Behauptungen (auch die heute so beliebten „gefühlten Wahrheiten“) anhand von Stichproben überprüfen. Klar, hundertprozentige Sicherheit böte nur eine Untersuchung der gesamten Population, doch das wäre ziemlich aufwändig. Auch bräuchte man dann keine Statistiker mehr, und ich wäre meinen Job los. Einfacher (und für mich einträglicher) ist es also, wir untersuchen nur Stichproben und beschreiben die verbliebene Unsicherheit als Wahrscheinlichkeitsrechnung. Hierfür starten wir mit einer Ausgangs- oder Nullhypothese (H₀), setzen dieser, damit sie nicht so einsam ist, eine gegenteilige Alternativ- oder Einshypothese (H_a) gegenüber, und schon kann es losgehen.

Untersuchung am leicht alkoholisierten Traditionsbeispiel

Zur Erläuterung von Hypothesentests wird gern das berühmte, aber etwas angestaubte Beispiel einer Lady Ottiline herangezogen, die behauptet, sie könne herausschmecken, ob zuerst der Tee oder die Milch in ihre Tasse gegeben wurde. Da ich selbst lieber Kaffee trinke (und zwar ohne Milch), schlage ich hier gern ein kleines Update mit schottischem Single-Malt-Whisky vor: Lady Ottiline behauptet also, sie könne schmecken, ob zuerst der Whisky oder das Wasser im Glas war. Zugegeben, ein Beispiel mit Erklärungsbedarf: Wahrscheinlich weiss nicht jeder, dass man einem Single-Malt meist ein paar Tröpfchen Wasser beigibt, aber warum nicht en passant ein bisschen Kultur vermitteln?

Wir geben der Dame also acht Gläser Whisky mit jeweils drei Tropfen Wasser und lassen sie kosten. Unsere H₀ lautet: Sie kann nicht entscheiden, welcher Bestandteil zuerst im Glas war. Dann wäre ihre Trefferquote bestenfalls 50 Prozent (p <= 0.5). Die entgegengesetzte H_a lautet: Sie kann es entscheiden. Dann müsste ihre Trefferquote grösser als 50 Prozent sein (p > 0.5). Um es kurz zu machen: Unsere Lady Ottiline ist zwar vielleicht irgendwann ein bisschen beschwipst, liegt aber bei allen 8 Gläsern richtig. Bei blossem Raten hätte ihre Trefferquote bestenfalls p ≈ 0.004  betragen dürfen (die Lesenden prüfen selbst nach). Wir verwerfen also unsere H₀ und akzeptieren die H_a. So weit, so einfach. Die Studierenden sind glücklich. Das haben sie verstanden.

Gewürfelte Wahrscheinlichkeiten

Dummerweise ist es damit nicht getan, denn mit dem bösen Wort Zufallsschwankungen wird es gleich ein bisschen komplizierter: An dieser Stelle nehmen wir mal an, wir wollen ins Spielcasino gehen, um entgegen allen Wahrscheinlichkeiten am Würfeltisch reich zu werden. Vor dem Eingang lungert ein windiger Typ herum, der uns eine spezielle Wurftechnik verkaufen will, durch die sich die Wahrscheinlichkeit eine 6 zu würfeln erhöhen soll. Natürlich verlangen wir eine Kostprobe von ihm und haben uns dafür mit Hypothesen bewaffnet. H₀: Der Typ will uns betrügen, also ist die Wahrscheinlichkeit für eine 6 bestenfalls 1/6, p <= 1/6. H_a: Er kann, was er behauptet, dann müsste die Wahrscheinlichkeit höher als 1/6, p >1/6 sein. Wir lassen den Kerl also 56-mal würfeln und zählen dabei die Sechsen. Er schafft 13, was einer relativen Häufigkeit von 0.232 entspricht und damit tatsächlich höher ist als 1/6=0.1667. Wow. Aber könnte es sich bei diesem Ergebnis vielleicht nur um eine Zufallsschwankung der Nullhypothese handeln? Das lässt sich berechnen, ist nur leider ziemlich kompliziert. Gönnen wir uns daher erst mal ein Schlückchen von Lady Ottilines Whisky und atmen tief durch, bevor wir das böse Wort Binominalverteilung (Abb. 1) aussprechen – wohl wissend, dass wir schon bei der Erläuterung dieser Formel die Hälfte der Studierenden verlieren werden, ganz egal, ob sie heimlich auch von Lady Otterlines Whisky genascht haben oder nicht.

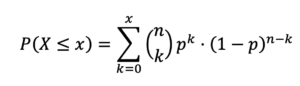
Abb.1: Binominalverteilung

Wie man Studierende glücklich macht

Wer gerne in leere Augen unter rauchenden Köpfen blickt, kann den jungen Leuten im Anschluss an diese Berechnung gleich noch eine zur Normalverteilung (Abb. 2) präsentieren, bei der mehr als nur zwei Werte angenommen werden können. Für echte Mathe-Nerds ist das vielleicht eine schöne Übung, den anderen jedoch (und das sind, von kleineren Zufallsschwankungen abgesehen, gewöhnlich alle) wird man damit jeden Spass an Statistik austreiben. Zu Recht. Denn sowohl für Binominalverteilung als auch für Normalverteilung gilt: Die gesuchten Wahrscheinlichkeiten können gar nicht manuell berechnet werden. Man braucht mindestens einen guten Taschenrechner oder möglichst gleich einen Computer. Und weil die Dinger zufälligerweise sowieso auf jedem Tisch stehen, spricht nichts dagegen, die Wirkung des Zufalls gleich maschinell simulieren zu lassen. Mit modernen Software-Paketen lässt sich das einfach umsetzen, und das Experiment in Sekundenschnelle zehntausendfach wiederholt werden – ganz ohne Rückgriff auf Binomialkoeffizienten und andere fiese Formeln. Glückliche Studierende!

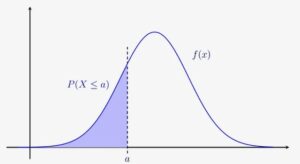
Abb. 2: Die Normalverteilung

Es lebe der Fortschritt!

Dank moderner statistischer Software mit didaktisch aufbereiteten Paketen lassen sich solche Simulationen mit intuitiven Keywords leicht umsetzen. Man muss nur ein paar Code-Snippets (um es mal neudeutsch zu formulieren) lernen, und kann – bei guter Anleitung – zudem GenAI für die Erstellung der Befehlszeilen nutzen. Meine Erfahrungen mit diesem Vorgehen in den Studiengängen des Departements Wirtschaft waren jedenfalls überaus positiv. Sofern überhaupt Probleme im Umgang mit dem Computer auftauchen, liegen diese weniger im Verständnis der Simulation. Die Studierenden scheitern eher mal daran eine Excel-Datei zu öffnen oder nach dem Abspeichern wiederzufinden. Aber das zu erlernen, kann ja wirklich nicht schaden. So wenig, wie ein paar Spritzer Wasser in einem guten Single-Malt. Aber bitte: immer erst den Whisky einschenken und sich tröpfchenweise rantasten!